こんにちは！

家庭教師のトライ大分校のブログ担当です。

今日のテーマ

◇◇◇◇　高校2年生用勉強法　◇◇◇◇

今回は高校2年生用の勉強法ついてご紹介していきます！

①「わからない」を解消する

②過去問に挑戦してみる

③頑張りすぎない

以下に詳しく説明していきます！

①「わからない」を解消する

高校2年生の間は少しずつでいいので、「わからない」を減らしていくことが大事です。

というのも高校3年生に入ると難しい単元の授業が多くなり、かつ共通テストや大学の過去問を解くことが必然と増えるため、復習に割く時間がなくなってきます。

高3のときのタスクを少しでも減らすために、高2のうちは復習メインで勉強しましょう。

自分のわからない単元や苦手なところがわからない場合は、問題集の目次を見て自信のない単元から手をつけてみることをおすすめします。

②過去問に挑戦してみる

復習ばっかりの勉強に飽きてきたら、自分に力量を測るために実際に大学や共通テストの過去問を解いてみましょう！

注意すべきは過去問を全部解くのではなく、自分の解ける単元の大問のみを解くことです。

無理に知らない単元を解いて自分のモチベーションを落とさないように気を付けてください。

過去問を解くことで自分の解けない問題を把握し、なぜ解けなかったのか分析することで大きく成長できるはずです！

③頑張りすぎない

ここまで勉強のアドバイスをしてきましたが、一番大事なのは高3に向けて今のうちにどこまで勉強することができるかです。

ほとんどの方は勉強をする前に“どこを勉強するか”や“いつするか”など、ある程度の計画を事前に立てると思います。

そしてその計画通りに勉強を進められない方も少なくないと思いますが、それでも自分を嫌いにならないでください。

一番ダメなのが自己嫌悪に陥り、勉強しなくなってしまうことです。

計画通りにいかなかった日は自分を追い込みすぎてないか計画を見直して、

「うまくいかない日もあるな」くらいに思って次からの勉強を頑張ってください。

繰り返しになりますが大事なのは今のうちにどこまで自分を成長させることができるかです。

毎日少しずつでいいのでコツコツ頑張りましょう！

いかがでしたでしょうか？

以上が高校2年生の勉強法における3つの大事なことでした。

3つ目で計画通りに勉強を進められない方は見直すように言いましたが、そういう方は完璧主義の人が多いと思います。

ここでいう完璧主義は自分の計画したとおりにできないと自己評価を下げてしまい、物事をうまく進められない人たちです。

私もその一人でした。

そこで意識していたことが「少しでもいいからやる」です。

たとえ前回の勉強が問題の途中で終わっていても、その途中から勉強を始めて、終わる時も切りのいいところまで解くのではなく、時間になったら終わるなどです。

「ここまでやらないと」という気持ちが私を勉強したくなくなるようにしていたことに気づいて、このように考えるようにしました。

実際タスクを始めるときは、前回の途中から入る方がより抵抗なく始められるそうです。

ですので完璧主義で悩んでいる方はぜひ真似してみてください！

家庭教師のトライでは自分に合ったスピード・やり方で成績を伸ばすことができます。

あなたの力になれることが私たちの喜びです。お気軽にお問い合わせください！

こんにちは！

家庭教師のトライ大分校のブログ担当です。

今日の勉強テーマ

◇◇◇◇　数B平面ベクトル　◇◇◇◇

今回は数Ⅱ平面ベクトルついて、理解しておくべき点をご紹介していきます！

まず大事な点を5つ挙げます。

①平行条件

②分解

③内積

④共線・共点条件

⑤ベクトル方程式

以下に詳しく説明していきます！

①平行条件

まず覚えてほしい式が平行条件式です。

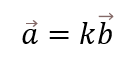
これを満たすkが存在するときベクトルaとベクトルbが平行だといえます。

平行を証明させる問題はたくさんありますのでしっかり覚えておきましょう。

②分解

うろ覚えで前後がぐちゃぐちゃになりやすいベクトルの分解です。

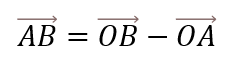
（後）ー（前）で覚えましょう。

ベクトルのほとんどの計算問題で使います。

とくに正六角形のベクトルの分解では、これを覚えてないと絶対といっていいほど解けないです。

③内積

内積はベクトルの中で一番理解しがたい概念だと思います。

しかし概念まで理解しなくとも、テストで点を取ることはできます！

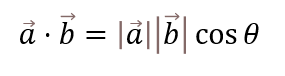
内積の公式はベクトルの公式の中で唯一角度を含みます。

そのため問題で角度が出てきたら、内積を使うんじゃないかと疑ってください。

またベクトルの角度の問題では余弦定理を使う場面もありますので、解法の一つとして覚えておいてください。

④共線・共点条件

共線条件

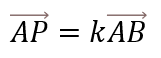
点Pが直線AB上にあるとき、このように表すことができます。

平行条件に似ているので比較的覚えやすい公式です。

共点条件

3直線 l, m, nが1点で交わるとき、lとm, mとnの交点が一致する。

これが共点条件です。

具体的には lとmの交点と mとnの交点の座標を求めて、それらが一致するとき3直線 l, m, nが1点で交わると証明できます。

⑤ベクトル方程式

1. 定点Aを通り、ベクトルdに平行な直線p

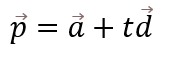
2.定点Aを通り、ベクトルdに垂直な直線p

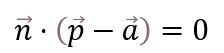
3.異なる2点A, Bを通る直線p

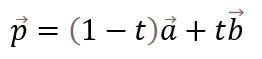
これら3つはどれも重要ですが、どれがどの式か混乱しやすいのでしっかり区別して覚えましょう。

・円のベクトル方程式

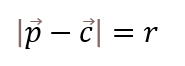
これはベクトルpとベクトルcの距離がrという意味です。

つまりベクトルpの軌跡をたどると、中心c半径rの円が出来上がります。

大事なのは下線部分ですので、そちらをしっかり理解してください。

いかがでしたでしょうか？

以上が平面ベクトルにおける5つの大事なことでした。

平面ベクトルの内容は、数Ⅲでやる複素数と内容が似ています。

そのためここをしっかり理解できると、後々楽になります。

またベクトルはほとんどの大学の二次試験ででますので、今のうちから対策しておいてください。

家庭教師のトライでは自分に合ったスピード・やり方で成績を伸ばすことができます。

あなたの力になれることが私たちの喜びです。お気軽にお問い合わせください！