みなさんこんにちは。家庭教師のトライ　愛知本部です。
だんだんと寒さが消え、春の兆しが少しずつ見え始めてきました。
4月になったら新学年がはじまります。みなさんいかがお過ごしでしょうか。

さて、今回は3月8日と12日に行われた愛知県公立高校入試の分析と、
やや難易度の高かった問題の解説を行いたいと思います。

【Ｂ日程　数学問題の解説】



こちらでは大問３で出題された空間図形の問題について解説していきます。
①は球の表面積を求める問題ですので公式に則って計算をしていけば解ける問題です。
②が少々難しかったのではないでしょうか。今回は②を解説していきます。

この問題で求める答えは正三角柱ABCDEFの体積です。
まずおさらいしましょう。正三角柱の体積の求め方は「底面積×高さ」でした。

球が正三角柱に内接しているため、高さは球の直径と等しいことが分かります。

そのため、高さは４cm。

続いて求めなければいけないのは底面積。
この底面積を求めることに苦労した受験生は多いのではないでしょうか。

底面積を求めるためにはこの図形を「空間」ではなく「平面」として捉える必要があります。

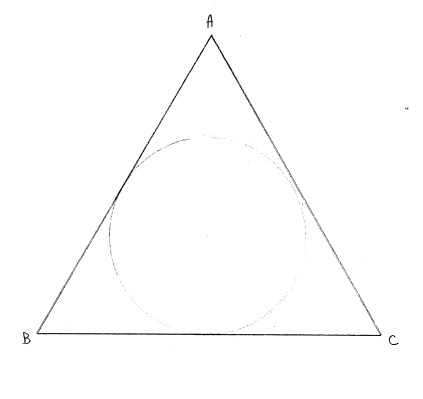
▼こちらの図を見てください。

これはこの立体を上から見た図になります。正三角形の中に円が内接している図が見て取れます。
正三角形の角の二等分線を引くと垂直に辺を二等分するという性質がありました。



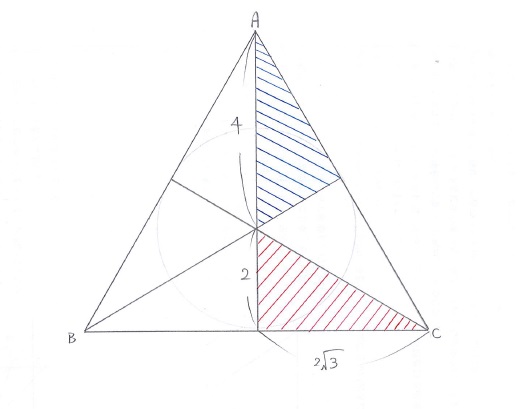
▲この図は３つの角の二等分線を引いたものになります。

複数の直角三角形が出てきました。この直角三角形は1:2:√3の直角三角形です。

三角形の面積の求め方は
底辺×高さ÷２
直角三角形の比を使いながら底辺と高さを求めていきましょう。

まずは高さを求めていきます。
赤色の三角形は一部が円の半径と重なるため、長さは２cmになります。
続いて青色の三角形の斜辺に注目しましょう。1:2:√3の比から斜辺の長さは４cmです。
つまり高さは６cmになります。

続いて底辺を求めましょう。
底辺は赤色の三角形の2√3cmの長さの２倍です。なので底辺は4√3cm。

つまり面積は、
4√3×6÷2＝12√3　になります。

これで体積を求められます！式はこのようになります。
12√3×4＝48√3

いかがでしたでしょうか。
「視点」を変えることが大切です。
この問題は相似を使って解くこともできます。
ぜひ色々な解法にチャレンジしてみて下さい。

◆これから高校受験を迎える中１・２年生・小学生の皆さんへ

ここ数年、公立入試は2020年の教育改革の方針の合わせた出題傾向になってきています。
「思考力」、「判断力」、「表現力」この3観点が大きく問われているのではないかと分析できます。
記述量の増加や普段見慣れない統計資料からの出題があったように知識だけでは勝負できません。
ゆえに、知識をどう運用していくのかという能力が今後求められてくるでしょう。

これから受験生になる方はぜひ、「アウトプット」を意識してみてください。
知識を入れ込む「インプット」だけではただ知識を得ることで終わってしまいます。
学校の友人や親御さんに協力してもらい、得た知識を実際に口に出して説明してみましょう。
そのときに意識するべきことは「知識と知識をつなぎ合わせるように論理的に説明する」です。

説明できるという行為は知識の運用力を高めると共に、本当に理解している証拠にもなります。
これがトライの家庭教師・個別教室で行っているダイアログ指導です。
是非みなさん取り入れてみてください。



トライでは受験に向けたトライさんによる進路相談・学習相談を無料で行っています。
この４月からの受験生に限らず、それ以外の学年の生徒さんも大歓迎です。
是非お気軽にお問い合わせください。