群馬県の皆さん、こんにちは。

今回は、学期末テストに向けた学習法～数学～　中学2年生向けをお伝えします。

テーマは1次関数。

1年生で学んできた「比例・反比例」の発展したものが1次関数です。

苦手だからいいや…と諦めてしまうと、中学3年生の授業、そして入試でとても苦労します。

苦手を克服しなかったことを後悔するでしょう。

ぜひ中学2年生の1次関数をマスターして、中学3年生の2次関数へつなげていきましょう。

1次関数では、y=ax+bの式に表わして、あるxの値に対応するyの値を求めたり、

yがある値をとるときのxの値の求め方を学んでいきました。

そこで、例題を取り上げて、復習をしつつ、ポイントを押さえていきましょう。



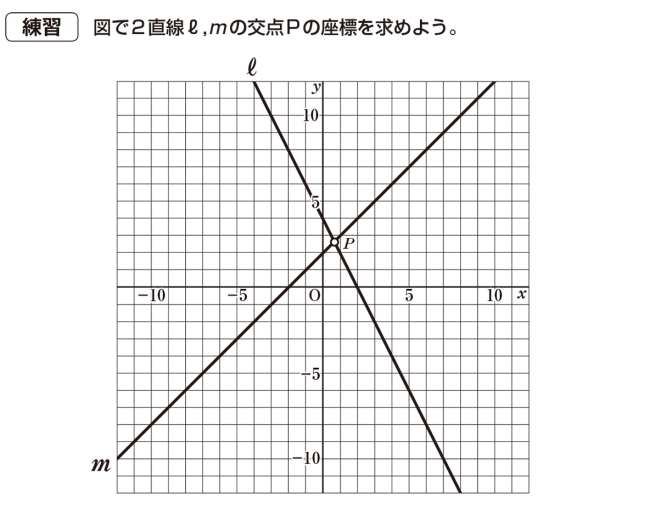
さて、あなたは解くことができるでしょうか？

《解法手順》

2直線の式が分かれば、交点の座標が求められるので、

①2直線の式を求める

②2直線の式を連立方程式として解く　⇒　求められたxとyの値が交点の座標になる

という流れになります。

今回は、1次関数がテーマなので、直線の式の求め方のポイントを押さえていきましょう。

グラフから考える直線の式の求め方

直線の式は　ｙ＝ax+b　これが基本形となります。

aは傾き（変化の割合）、bは切片（ｙ軸との交点）。この2つを読み取れればOKです。

★直線 l

・傾き：ｘが右に1、下に-2。つまり傾き（＝変化の割合）は、ｙの増加量/xの増加量=-2

・切片：ｙ軸との交点⇒４

よって、直線ｌはｙ＝ax+bに、a=-2、b=4を代入して、y=-2x+4とわかります。

★直線 m

直線ｍを求めると、傾きが1、切片が2なので、直線ｍはｙ＝ax+bにa=1、b=2を代入して

y=1x+2とわかります。

…気づきましたか？

直線ｍの答え方、間違っています。

y=1x+2ではなく、正しくは、y=x+2です。

ここで気づいた方はばっちりです！1xと書いてしまう人、実はとても多いのです。

わかっていても、テストで焦ってしまって…ということがありますので、気をつけましょう。

上の問題は、TryIT問題集より引用しました。

さらに詳しい解答とTryIT無料動画｢１次関数と連立方程式がからむ問題」は下記URLから

視聴いただけます。

https://www.try-it.jp/chapters-812/sections-851/lessons-860/practice-3/

トライでは、３０周年キャンペーンとして

全コース入会金無料キャンペーンを行っています。

ぜひ、お気軽にお問い合わせください。

※受付期間2017年3月31日まで。